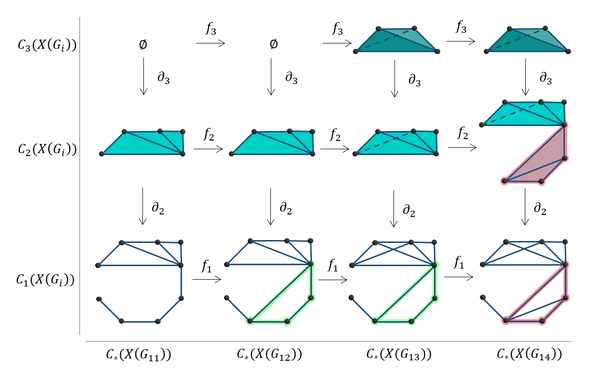
A classical area of mathematics called algebraic topology brings us a way to study the topological cavities of objects. This method is called homology.
Homology can be computed on the clique complex of a graph. The clique complex is an enrichment of a biniary graph G(V,E) made of cliques - all-to-all connected subgraphs - contained in the graph G.
Homology allows us to (roughly) count the number of cavities in each dimension of the clique complex. These cavities are surrounded by a loop of cliques called a cycle. The cycle also carries an indication of the dimension of the cavity it surrounds; a loop around a 2D cavity is called a 1-cycle, a loop of 3-cliques (triangles) around a 3D cavity is a 2-cycle, and so on.
|
Maps between graphs in a filtration induce maps on the homology groups, meaning we can track homology groups along the filtration. This computation is called persistent homology, and is rigorously described elsewhere (Carlsson 2009, Ghrist 2008, Zomorodian and Carlsson 2005). Colloquially persistent homology allows us to follow the evolution of topological cavities throughout the filtration. We can record the number of d-dimensional cavities at each point in the filtration, which yields a curve for each dimension called the Betti curve. |